No 21 by Child’s Play
Puzzle explanation
This is one possible solving path. Because we know the grid will eventually be converted from numbers to the letters used in the clues, each cell can only contain a number from 0 to 16. As there are only seven two-digit cells, each of the numbers 10 to 16 must appear in exactly one cell. We’ll use the notation “12|3” to show how numbers may be partitioned into cells.
Using the facts that clue answers are in ascending order in each list and the numbers of cells used are given, we can establish some limits for each answer. For example, 12ac must have three digits, because a four-digit answer would make all the answers up to 18ac also have at least four digits, requiring eight or more two-digit cells in total.
In the clues, every letter is added, subtracted or multiplied somewhere and therefore isn’t allowed to be 0 (which would make the operation trivial), except for M, which appears only in 33dn as a factorial, so M = 0 (making M! = 1). All the remaining letters except O participate in a multiplication somewhere and therefore can’t be 1, so O = 1.
The single-letter clues 5, 7, 20 and 21 show that C, L, T and I are two-digit numbers, with T < I and C′ < L′. I′ appears in clue 14, and K′ in clue 33, so to be reversible they’re restricted to the range [12, 16], as are C and L. C′ and L′ both end in 1 and C′ < L′ means the other digit of C is less than the other digit of L, therefore C < L with C in the range [12, 15] and L in [13, 16].
For clue 3, C + K ≤ 15 + 16 = 31. The value for clue 2 has to be smaller, ie IN < 31 with I ≥ 12, so N = 2. Now clue 2 is 2I ≥ 2×12 = 24. Clue 5 has to be greater, so C′ ≥ 31 and C is one of {13, 14, 15}, pushing L′ up, with L in {14, 15, 16}. Clue 10 has to be greater than L′ ≥ 41, so A! > 41 and A ≥ 5 (since 4! = 24 is too small). If A is 6 then clue 16 ≥ 6×36 = 4374, which can’t be split into two cells with values ≤ 16. Therefore A = 5. Now if E is 4 then clue 16 = 5×45 = 5120, also too big to fit into two cells, so E = 3 and clue 16 = 12|15 (to be entered in two cells).
For clue 29, if F is 6 the minimum is 65 − 16×15 = 7536, too big to fit into two cells with valid values, so F < 6 and the only available value is F = 4. The minimum for clue 6 is now 13 + 4×10 = 53, which means clue 7 = 61 with L = 16. Now C and K are both ≤ 15, so the maximum for clue 3 is 14 + 15 = 29, making clue 2 = 2I at most 28, so I is one of {12, 13, 14}. But clue 13 = (15I)′ and if I is even then 15I would end in 0 and not be a valid reversible number, so I = 13, making clue 2 = 26, clue 13 = 591, clue 14 = 713 and of course clue 21 = 13.
C and K are now both in {12, 14, 15} and C + K (clue 3) must be > 26 (clue 2); the only possible sums are {12 + 15 = 27, 14 + 15 = 29}. If the sum is 27 then clue 15 is (27×25)′ = 468, but its value needs to be > 713 (clue 14). Therefore {C, K} = {14, 15} and C + K = clue 3 = 29, making clue 15 = 829 and clue 25 = 116 (to be entered in two cells either as 11|6 or 1|16). If C is 14 then clue 28 is (14×3×7)′ = 492, but that can’t be fitted into two cells because neither 49 nor 92 is a valid cell value. Therefore C = 15, K = 14, clue 28 = 513 and clue 5 = 51.
Clue 10’s value 120 − (13R)′. Clue 9 is 2R2 and has to be between 61 (clue 7) and 120, so it’s one of {2×62 = 72, 2×72 = 98}. If R is 6 then IR is 13×6 = 78, but 120 − 87 = 33 is too small for clue 10. Therefore R = 7, clue 10 = 10|1 and clue 9 = 98.
Clue 17 = (G! + 434)′. If G is 8 then its value is 45704, which has to fit into three cells, but no pair of adjacent digits is a valid cell value; therefore G can’t be 8. If G is 9 then 9! = 362880, but fitting a six-digit number into three cells would need three double-digit cells for this and the next clue, bringing the total of double-digit cells to eight (as clue 16 is 12|15), too many. Therefore G < 8 and the only available value is G = 6, making clue 17 = 4|5|11.
T < 13 (clue 21), ie T is one of {10, 11, 12}. If T is 10 then clue 11 = 12T = 12|0, but clue 16 = 12|15 has a cell containing 12 and there can be only one among the across answers, so T isn’t 10. If T is 12 then clue 6 = 4T + 15 = 63, but it should be < 61 (clue 7), so T isn’t 12. Thus T = clue 20 = 11, clue 6 = 59, clue 11 = 13|2 and clue 31 = 6|7|10.
The remaining values for Y are {8, 9, 10, 12}, giving clue 32 = (16Y − 1)7Y the respective values {7112, 9009, 11130, 16044}. Both 9|0|0|9 and 16|0|4|4 would need at least four cells but only three are available; 11|13|0 could fit in three cells, but there’s already a cell containing 13 in a down answer (clue 28 = 5|13). So the only possibility left is clue 32 = 7112 (either 7|11|2 or 7|1|12) with Y = 8. Clue 8 is B2 − 2 and has to be between 61 (clue 7) and 98 (clue 9), and the only available value is B = 9, making clue 8 = 79, clue 1 = 17 and clue 22 = 63.
The remaining values for D and J are {10, 12}. From clue 23 = (9 + D)(J − D)2, J − D has to be positive, so J = 12 and D = 10, completing the rest of the algebraic clues: clue 4 = 40, clue 12 = 156, clue 18 = 6|8|14, clue 23 = 76, clue 24 = 81, clue 26 = 237, clue 27 = 295, clue 29 = 9|14, clue 30 = 940 and clue 33 = 8|15|9.
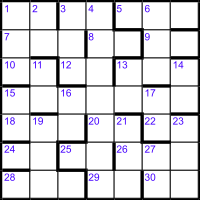
For convenience in describing the filling of the grid, we’ll add entry numbers as shown. Sorted by the number of cells to occupy, we have the following answers:
| Across | Down | ||
|---|---|---|---|
| 17 | 156 | 11 | 237 |
| 26 | 591 | 13 | 295 |
| 29 | 713 | 63 | 940 |
| 40 | 829 | 76 | 6|7|10 |
| 51 | 4|5|11 | 81 | 7|11|2 or 7|1|12 |
| 59 | 6|8|14 | 1|16 or 11|6 | |
| 61 | 8|15|9 | ||
| 79 | 5|13 | ||
| 98 | 9|14 | ||
| 10|1 | |||
| 13|2 | |||
| 12|15 | |||
Concentrating on the two-digit cells, we have 12|15 across and 8|15|9 down, and there can be only one 15 cell in the grid, so they have to cross. The only place where the second cell of a two-cell across entry is the middle cell of a down entry is at 24ac/19dn. Then 28ac can only be 591 and 18ac = 6|8|14 with 9|14 at 16dn.
The places where 6|7|10 (down) and 10|1 (across) can cross are 1dn/10ac and 3dn/12ac, so 7ac either starts or ends with 7. But there’s no three-cell across value ending in 7, so 7ac = 713, 1dn = 6|7|10, 10ac = 10|1, 1ac = 61, completing 2dn = 11, and 3dn = 237 with 12ac = 79.
The places where 5|13 (down) and 13|2 (across) can cross are 17dn/22ac and 27dn/30ac, so 23dn either starts or ends with 2. If it’s 295 then there’s no across value to fit _5 at 30ac. Therefore 23dn ends in 2 and can only be filled by 7|11|2 (eliminating both 7|1|12 and 11|6 as possible down entries), which makes 22ac = 17, 30ac = 13|2, 27dn = 5|13, 26ac = 4|5|11, 21dn = 940 and 29ac = 40. Since 11|6 has been eliminated, _6 at 15dn now has to be 76.
The only value left for _1 at 17dn is 81. The only unplaced three-cell down value is 295, so that must go at 6dn, making 3ac = 829, 9ac = 98, 13ac = 156 and 14dn = 63.
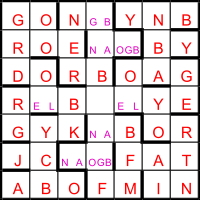
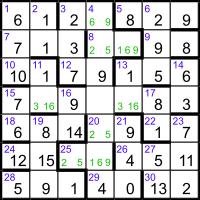
We now have most of the grid filled, missing only the central seven-cell entries and some of the two-cell numbers crossing them, as shown. The reverse of 15ac is either 3861_937 or 383_9617, but before testing the 20 possible values for being the product of a square and a prime, let’s look at the letter version of the grid.
We know the 49 letters will produce 10 words, so the average word length is 4.9, but there are almost no potential words longer than three letters reading across or down. Turning to diagonals, we might notice that GORDON can be traced contiguously in the NW corner, with MARTIN symmetrically opposite, JACK in the SW corner and possibly BOBBY in the NE. In the same diagonal zigzagging pattern there’s GEOFF preceding MARTIN and a potential GEORGE after GORDON. That may be enough to suggest the England football team that won the FIFA World Cup in 1966, with NOBBY Stiles, BOBBY Moore and BOBBY Charlton explaining the preponderance of Bs and Ys in the grid. In fact, it happens that the names are listed in increasing order of the players’ shirt numbers, with only ROGER Hunt missing, in shirt No 21, the puzzle’s title.
Filling in the gaps to complete the list of names makes the unresolved two-letter entries NG, AO, AB and NB (across), and OE and OL (down), which do correspond to the unplaced clue values 26, 51, 59, 29, 13 and 1|16 respectively.
The alternative approach is laborious, factorising the possible values from the long grid entries. Of the 20 possible values from (the reverse of) 15ac, three are the primes {38610937, 38613937, 38614937}, but then the “square” in the clue would be 12 = 1, giving a trivial multiplication that’s disallowed in the preamble. The only other value that’s a square × a prime is 38619937 = 172×133633, making 15ac = 73991683 (with 16 in the fifth cell) with 11dn = 13 and 13dn = 1|16.
3ac is either 26 or 29. If it’s 29 then 26ac has to be 59, and 8ac and 25ac are {26, 51} in either order, making 4dn one of {9299514, 9599564}. The corresponding reverses are {4159929 = 3×1386643, 4659959 = 19×245261}, neither having a square factor, so 3ac = 26. There are four permutations of the remaining values {29, 51, 59} among 8ac, 20ac and 25ac, making 4dn one of {6299514, 6599214, 6599294, 6599594}. All four of the reverses have a square divisor, {4159926 = 32×2×231107, 4129956 = 62×89×1289, 4929956 = 22×71×17359, 4959956 = 22×1239989}, but only the last has just one other prime factor. So 4dn = 6599594, with 8ac = 51, 20ac = 59 and 25ac = 29, completing the grid.

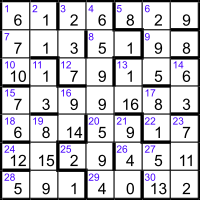
Converting the numbers to letters, the 10 names can be read in shirt order as above: GORDON (Banks = 1), GEORGE (Cohen = 2), RAY (Wilson = 3), NOBBY (Stiles = 4), JACK (Charlton = 5), BOBBY (Moore = 6), ALAN (Ball = 7), BOBBY (Charlton = 9), GEOFF (Hurst = 10) and MARTIN (Stanford Peters = 16).
The puzzle’s title referred to number 21 as Roger Hunt’s shirt, the fact that the grid contained no (name of the player wearing shirt) 21, and incidentally that the letters NO in the clues stood for 2 and 1. The puzzle was published the day before the final of the 2023 FIFA Women’s World Cup, in which England’s Lionesses sadly failed to repeat the success of 1966.
