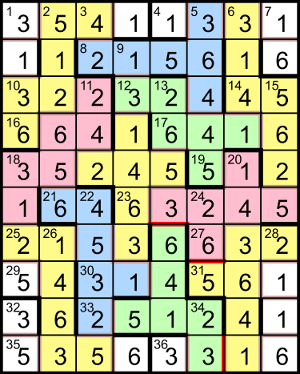
Dice Nets by Arden
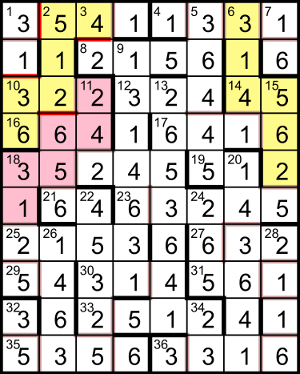
Puzzle explanation
There are 11 different shapes that can be folded to make a cube and all were used for the dice nets. On a standard die the sum of numbers on opposite faces is 7, which restricted the possibilities for the nets. All the nets in the grid would form “left-handed” dice if they were folded away from the viewer, or right-handed ones if folded toward the viewer (ie, with the numbers on the inside).
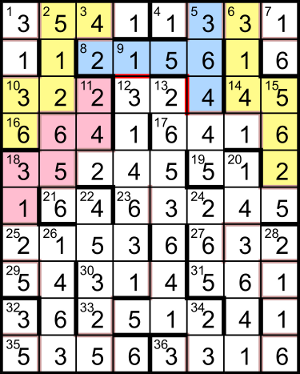
Puzzle solution process
This is one possible solving path. Since the grid’s digits are restricted to 1 to 6, any prime entries must end with 1 or 3, and squares must end with one of {1, 4, 5, 6}. The nth triangular number is given by n(n + 1)/2; the product of any two consecutive integers ends in one of {0, 2, 6} (0×1 = 0, 1×2 = 2, 2×3 = 6, 3×4 = 12 etc), so any triangular number ends in one of {0, 5, 1, 6, 3, 8}, of which only {1, 3, 5, 6} are valid in the grid.
7dn and 21ac are two-digit powers (cubes or higher); of the candidates {24 = 16, 25 = 32, 26 = 43 = 64, 33 = 27, 34 = 81}, the only ones consisting of digits 1 to 6 are {16, 32, 64}. 4ac and 18dn are four-digit powers; the powers of 2 in the range from 1111 to 6666 are {2048, 4096}, both with invalid digits; the powers of higher numbers are {37 = 2187, 38 = 6561, 55 = 3125, 64 = 1296, 74 = 2401, 113 = 1331, 123 = 1728, 133 = 2197, 143 = 2744, 153 = 3375, 173 = 4913, 183 = 5832}, which all have invalid digits except for {1331, 3125, 6561}. The only digit that can be at the end of 4ac and the start of 7dn is 1, so 7dn = 16, with 4ac being one of {1331, 6561}. 21ac is now one of {32, 64} but 2dn is a square and can’t end with 3, so 21ac = 64.
6dn starts with 3 or 6 and is 18dn + 16, so 18dn is one of {3125, 6561}; but if it’s 6561 then 6dn starts with 6 and 4ac also has to be 6561. So 18dn = 3125 and 6dn = 3141, which makes 4ac = 1331.
Now 14ac is a triangular number matching 4_, which can only be 14ac = 45 (the 9th triangular number, as 9(9 + 1)/2 = 45). 17ac is a multiple of 16 (7dn), so it’s even, and 15dn is a square matching 52__, 54__ or 56__. The only two such squares are {5476, 5625} and the only one with valid digits is 15dn = 5625.
29ac is a multiple of a power, matching 5_; the possible values are {2×33 = 54, 7×23 = 56}. 19ac + 29ac is a triangular number, in the range from 11 + 54 = 65 to 66 + 56 = 122. Since the nth triangular number is given by T = n(n + 1)/2, n and n + 1 are the integers immediately below and above √(2T). For the range 65 to 122, the limits for n are √(65×2) ≈ 11.4 and √(122×2) ≈ 15.6, ie the potential triangular numbers are {11×12/2 = 66, 12×13/2 = 78, 13×14/2 = 91, 14×15/2 = 105, 15×16/2 = 120}. If 29ac is 54 the candidates for 19ac are {12, 24, 37, 51, 66}; if 29ac is 56 the candidates are {10, 22, 35, 49, 64}; the valid possibilities for 19ac are then {12, 22, 24, 35, 51, 64, 66}. But 32dn = 19ac − 16 and of the corresponding values {-4, 6, 8, 19, 35, 48, 50} the only valid one is 32dn = 35, making 19ac = 51 and 29ac = 54.
22dn is 4____ in the grid and it’s a multiple of 352 = 1225; the only multiples in the range 41111 to 46666 are {41650, 42875, 44100, 45325, 46550}, of which only 22dn = 45325 has valid digits. Now 35ac is a triangular number matching 5_5_; for triangular numbers T from 5151 to 5656, the values of n = (the integer just below) √(2T) are 101 to 106, giving the numbers {5151, 5253, 5356, 5460, 5565, 5671}, only the first three of which match 35ac. So 26dn, which is half a triangular number, matches _4_1, _4_2 or _4_3; the first two aren’t possible because a triangular number can’t end in 2 or 4, which means 35ac = 5356.
Twice 26dn ends in 6, and a triangular number n(n + 1)/2 can end in 6 only if n ends in one of {1, 3, 6, 8}. If 26dn starts with 1, the potential triangular numbers are from 2×1413 = 2826 to 2×1463 = 2926, with n in {75, 76}; 75 ends with the wrong digit but 76(76 + 1)/2 = 2926 works. If 26dn starts with 2, the range for n is {98, 99}; 99 has a wrong last digit and 98(98 + 1)/2 = 4851 doesn’t end in 6. If 26dn starts with 3, the range for n is {116, 117}, but 116(116 + 1)/2 = 6786, half of which is 3393, not matching 26dn. If 26dn starts with 4, the range for n is {132, 133}, but 133(133 + 1)/2 = 8911, not ending in 6. If 26dn starts with 5, n can only be 147, which has a wrong last digit; the same is true if 26dn starts with 6, with n = 160. Therefore the triangular number is 2926 and 26dn = 1463.
The prime 25ac is now 215_, ending in 1 or 3; 2151 is a multiple of 3 (as its digit sum is 9, a multiple of 3), so 25ac = 2153.
11dn is twice a square, so it must end in 2, with the square ending in 1 or 6. The square is in the range [112/2 = 56, 662/2 = 331], ie one of {81, 121, 196, 256}, with corresponding values {162, 242, 392, 512} for 11dn, of which only {162, 242, 512} have valid digits. The square 2dn ends in 6, so its square root must also be even and thus 2dn is a multiple of 4, which means its last two digits are a multiple of 4 (because every multiple of 100 is divisible by 4), ie 2dn ends in one of {16, 36, 56}. 18ac is now a five-digit triangular number starting with 312, 332 or 352. If it’s in the range [31211, 31266] the corresponding n is one of {249, 250}, giving triangular numbers {31125, 31375}, neither of which has 2 as the third digit; if it’s in the range [33211, 33266] the corresponding n is 257, giving the triangular number 33153, which also doesn’t have 2 as the third digit; so 18ac must be in the range [35211, 35266], with n = 265, giving the triangular number 18ac = 35245.
3dn is a two-digit product of three different primes. 3×5×7 = 105 is too big, so one of the primes is 2. The other two primes can’t include 5, or 3dn would end in 0. The only possible values in the range [11, 66] are {2×3×7 = 42, 2×3×11 = 66}. So 8ac starts with 2 or 6 and 8ac + 35245 (18ac) is a triangular number. If it starts with 2, triangular numbers in the range [2111 + 35245 = 37356, 2666 + 35245 = 37911] have values of n in the range [273, 275], giving triangular numbers {37401, 37675, 37950}, with {2156, 2430, 2705} for 8ac; if 8ac starts with 6, triangular numbers in the range [41356, 41911] have values of n in the range [287, 289], giving triangular numbers {41328, 41616, 41905}, with {6083, 6371, 6660} for 8ac. The only valid value for 8ac is therefore 8ac = 2156, which makes 3dn = 42.
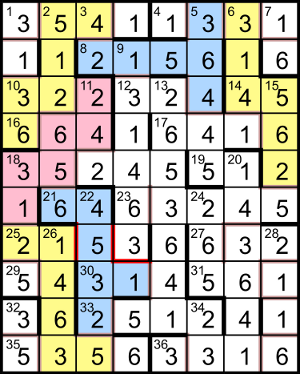
2dn is a square ending in 56, so its square root ends in 4 or 6. If the root ends in 4, it’s of the form 10x + 4 and its square is 100x2 + 80x + 16; for that to end in 56 needs 80x to end in 40, ie x ends in 3 or 8, meaning the root ends in 34 or 84. If the root ends in 6, it’s of the form 10x + 6 and its square is 100x2 + 120x + 36; for that to end in 56 needs 120x to end in 20, ie x ends in 1 or 6, meaning the root ends in 16 or 66. To summarise, the square root ends in one of {16, 34, 66, 84}.
If 2dn starts with 1, its root is between √111156 ≈ 333.4 and √166656 ≈ 408.2, ie one of {334, 366, 384}; if it starts with 2, the root is between √211156 ≈ 459.5 and √266656 ≈ 516.4, ie one of {466, 484, 516}; if it starts with 3, the root is between √311156 ≈ 557.8 and √366656 ≈ 605.5, ie one of {566, 584}; if it starts with 4, the root is between √411156 ≈ 641.2 and √466656 ≈ 683.1, ie 666; if it starts with 5, the root is between √511156 ≈ 714.95 and √566656 ≈ 752.8, ie one of {716, 734}; if it starts with 6, the root is between √611156 ≈ 781.8 and √666656 ≈ 816.5, ie one of {784, 816}. The squares of the potential roots are {133956, 147456, 217156, 234256, 266256, 320356, 341056, 443556, 512656, 538756, 614656, 665856}, of which only {234256, 266256, 443556, 512656, 614656} have valid digits for 2dn.
From the clues for 16ac and 31ac, we know that 16ac + 31ac is both a square (ending in {0, 1, 4, 5, 6, 9}) and a triangular number (ending in {0, 1, 3, 5, 6, 8}), so it ends in one of {0, 1, 5, 6}. 16ac starts with one of {1, 4, 5, 6}, because 1dn is a square; its middle digit is one of {2, 5, 6}, from 2dn; and it ends with one of {1, 4, 6}, from 11dn. 24dn is the sum of two consecutive squares, so it’s odd, and 31ac starts with one of {1, 3, 5}. Thus 16ac + 31ac is in the range [121 + 111 = 232, 666 + 566 = 1232], so as a square it’s in the range [162 = 256, 352 = 1225], the ones ending in {0, 1, 5,6} being {225, 256, 361, 400, 441, 576, 625, 676, 841, 900, 961, 1156, 1225, 1296}. Of those, the only one that’s also triangular, ie T = n(n + 1)/2 where n and n + 1 are the integers surrounding √(2T), is 1225 = 352 = 49×50/2.
Since 16ac + 31ac = 1225 and 31ac <= 566, 16ac must be ≥ 659, ie it starts with 66. It can’t be 666 because 1225 − 666 = 559 is invalid for 31ac, so 16ac is one of {661, 664} with 31ac in {564, 561} respectively. 11dn is now reduced to {242, 512} and 2dn to {512656, 614656}. Now 1dn is a square ending in 6, so the penultimate digit must be one of {1, 3, 5} as for 2dn above. 10ac must have the two-digit prime 34dn as a factor. If 11dn is 242, 10ac is one of {142, 322, 342, 522, 542} and dividing by 2 gives {61 = prime, 71 = prime, 161 = 7×23, 171 = 32×19, 261 = 32×29, 271 = prime}; if 11dn is 512, 10ac is one of {125, 145, 325, 345, 525, 545} and dividing by 5 gives {25 = 52, 29 = prime, 65 = 5×13, 69 = 3×23, 105 = 3×5×7, 109 = prime}. The two-digit primes with valid digits among those are {13, 23, 61} for 34dn, limiting 10ac to {122, 322, 325, 345}.
24dn is n2 + (n + 1)2, ending in 5, so n ends in one of {1, 3, 6, 8}; the only three-digit values up to 666 are {145, 265, 365, 545}. Now 27ac starts with 4 or 6 and 27ac + 16ac is a square in the range [661 + 411 = 1072, 664 + 666 = 1330], ie one of {1089, 1156, 1225, 1296}. Subtracting the two values for 16ac from those gives {425, 428, 492, 495, 561, 564, 632, 635}, of which only {425, 632, 635} are valid for 27ac. The corresponding values for 16ac are {664, 664, 661}, with 31ac in {561, 561, 564}. So the square 28dn matches one of {51__, 21__, 54__} respectively. Between √5111 ≈ 71.5 and √5166 ≈ 71.9 there are no integers; nor are there any between √5411 ≈ 73.6 and √5466 ≈ 73.9; so the square root of 28dn is between √2111 ≈ 45.9 and √2166 ≈ 46.5, ie 46, which makes 28dn = 2116, 27ac = 632, 31ac = 561, 16ac = 664 and 11dn = 242.
10ac is now limited to {122, 322}, which makes 2dn = 512656 and reduces 10ac’s factor 34dn to {23, 61}. 24dn is one of {265, 365} and 30ac = 3__ is 24dn + a square. If 24dn is 365, 30ac must be 365 + 12 = 366; otherwise 24dn is 265, and adding the squares from 36 to 100 gives {301, 314, 329, 346, 365}, of which only {314, 346, 365} are valid for 30ac. We can rule out 346 because 9dn is triangular and therefore can’t end in 4; also, 365 is no good because it would make the multiple at 33ac end in 0 or 5, whereas it has to end in 2 or 6, the first digit of 34dn. Therefore 30ac is one of {314, 366}. For 33ac, the four-digit multiples of 314 starting with 2 are {2198, 2512, 2826}, the only valid one being 2512, while the multiples of 366 are {2196, 2562, 2928}, with only 2562 valid. With 366 and 2562, the square at 13dn would end in 66, but (as above) a square ending in 6 must have {1, 3, 5} for its penultimate digit; therefore 24dn = 265, 30ac = 314, 33ac = 2512, 34dn = 23 and 10ac = 322.
Now 5dn is 36__5. The middle digit is the end of the even square at 12ac, ie one of {4, 6}. 17ac is a multiple of 16 matching __16, so 17ac − 16 (still a multiple of 16) ends in 00 and is automatically a multiple of 4; to be a multiple of 16 we need the first two digits on their own to be a multiple of 4; that is, 17ac is one of {1216, 1616, 2416, 3216, 3616, 4416, 5216, 5616, 6416}. Thus the fourth digit of 5dn is even, so 5dn is one of {36425, 36445, 36465, 36625, 36645, 36665}. We can quickly rule out the ones ending in 25, which have a repeated factor (5×5); of the rest, the only one with three prime factors is 36445 = 5×37×197, so 5dn = 36445. 17ac is now reduced to {2416, 4416, 6416}.
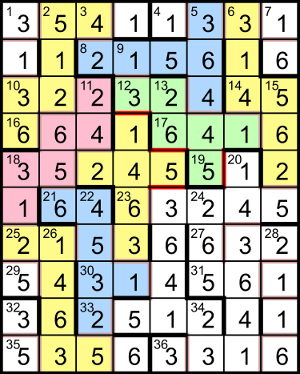
12ac now ends with 4 and the squares with valid digits in the range [114, 664] are {144, 324}. Now the square 13dn starts with one of {2, 4}, has {2, 4, 6} for the second digit, and matches __5__41. Its square root ends in 1 or 9. If it’s (10x + 1)2 = 100x2 + 20x + 1, then we need 20x to end in 40, ie x ends in 2 or 7; if it’s (10x + 9)2 = 100x2 + 180x + 81, then we need 180x + 80 to end in 40, ie x ends in 2 or 7 again; thus the root ends in one of {21, 29, 71, 79}. If it starts with 22, the root is between √2251141 ≈ 1500.4 and √2256641 ≈ 1502.2, but there are no numbers ending in {21, 29, 71, 79} in that range; for 24 the range is (1565.6, 1567.4), with no suitable numbers; for 26, (1628.2, 1629.9) contains 1629 and 16292 = 2653641 fits; for 42, (2061.8, 2063.2) has no suitable numbers; for 44, (2109.8, 2111.1) has no suitable numbers; for 46, (2156.7, 2157.9) has no suitable numbers. Therefore 13dn = 2653641, making 17ac = 6416 and 12ac = 324.
For the triangular 9dn we now have 13_4_31 in the grid. For n(n + 1)/2 to end in 31, n(n + 1) ends in 62, with n ending in one of {1, 3, 6, 8}. If the third digit of 9dn is 1, the “root” is between √(2×1314131) ≈ 1621.2 and √(2×1314631) ≈ 1621.5, giving 1621×1622/2 = 1314631, which fits; if the third digit is 2, the range for the root is (1627.3, 1627.7) but 1627 doesn’t end in one of the required digits; if the third digit is 3, the range is (1633.5, 1633.8) but 1633×1634/2 = 1334161 doesn’t fit; if the third digit is 4, the range is (1639.6, 1639.9) but 1639 doesn’t end in one of the required digits; if the third digit is 5, the range is (1645.7, 1645.98) but 1645 doesn’t end in one of the required digits; if the third digit is 6, the range is (1651.7, 1652.04) but neither 1651×1652/2 = 1363726 nor 1652×1653/2 = 1365378 has a middle digit of 4. Therefore 9dn = 1314631.
23ac is now 632_5 and is a multiple of 35; it’s clearly a multiple of 5 but it also needs 7 as a factor. Dividing 63215 by 7 leaves a remainder of 5; changing the fourth digit of that to get a remainder of 0 requires adding a (small) multiple of 10 that has a 2 remainder, ie 30 = 7×4 + 2, so 23ac = 63245. For the square 20dn we now have 1436__. The square root is between √143611 ≈ 378.96 and √143666 ≈ 379.03, ie 379 only; so 20dn = 143641 = 3792.
Now 36ac is _316 and is a jumble of __36 for 1dn, which means 1dn is either 1_36 or _136. 1dn is the square of a number ending with 4 or 6; if 1dn starts with 1, the square root is between √1136 ≈ 33.7 and √1636 ≈ 40.4 but neither 342 = 1156 nor 362 = 1296 fits; of the six possibilities for _136, the only square that fits is 1dn = 3136 = 562, which means its jumble 36ac = 3316. Then the prime 1ac is 354_; the digit sum of 3543 is 15, so it’s multiple of 3, which leaves 1ac = 3541 to complete the grid.
On a standard die the sum of numbers on opposite faces is 7, so any two adjacent numbers that add to 7 can’t be part of the same die. Nor can two adjacent digits that are the same, and we can add bars to separate such digits, as shown here.

Some cells in the corners of the grid are obviously not used and can be eliminated. For example, the 3 at the start of row 9 may connect to the 5 at the start of row 10 but it would then meet another 3. At the same time we can discount the 5s near the bottom of column 1 as neither could attach to an available 2 for a suitable net.

There are several places where there is a run of three cells, either straight or round a corner, that take the form XYX. In these cases the Y cannot be attached to both of the Xs and simple deductions add further forced bars. The most obvious example of this is the 141 run near the top of column 7: if the 4 were attached to the lower 1 it would be cut off, by the higher 1, from the only available 3 (top of column 7) to make a net. So a bar must be introduced between rows 3 and 4 in this column, which identifies the first complete net.
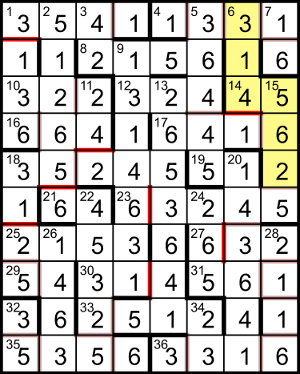
Of the available digits in the grid there are eleven each of 2, 4, 5 and 6, with twelve 1s and twelve 3s. If the solver is to maximise the number of nets at 11 they must use all of the 2, 4, 5 and 6 cells. So, for example the 6 in row 4 of column 1 can only be used in a single way, which defines its net as well as a second net cut off below it and also excludes the twelfth 1 and 3. Thus all the remaining nets can be delineated.