Word Squares by Elap

Puzzle solution process

This is one possible solution path. It’s useful to start by generating a list of the possible sums of squares, of which there are 28 (65 and 85 being sums of two different pairs of squares).

n510131720252629343740 414550525358616565687374 80828585899097
x11212312312 431423514235 4126534
y23344455566 567677687887 8997899

From 16ac = I2 with two digits, I < 10, so I = 5 and 16ac = 25. 12ac = A2 has three digits, so A > 10 (it can’t be 10 or 20 because then 12ac = 100 or 400 would make 13dn and 14dn start with 0) and A ≤ 31, ie A is one of {13, 17, 25, 26, 29} and 12ac is one of {169, 289, 625, 676, 841}. But 12ac = (D/P)2 is a two-digit square, so the overlapping values are 12ac = 16 and 12ac = 169, making A = 13. The grid now has 13dn = Y = 65.

We can enter (A − I)2 = 11dn = 64 and Y − A = 9ac = 52. The grid gives 17ac = 5_ and 14dn = 9_, both of which are sums of squares ending in the same digit, so they can only be 17ac = T = 50 and 14dn = 90.

17ac says 50 = (P − 13)2 + (S − M)2 and we know 50 = 12 + 72, so P − 13 is ±1 or ±7, which makes P one of {6, 12, 14, 20}. Only one of those is a sum of two squares, so P = 20 and S − M = ±1. We know 14dn = 90 = 32 + 92, so the clue tells us A + M − T = M − 37 is ±3 or ±9, ie M is one of {28, 34, 40, 46}, of which only {34, 40} are valid. But S = M ± 1, which only allows M = 40 and S = 41. That gives 3 for the second expression in 14dn, so the other one, M − I − R = 35 − R, must be ±9, ie R is one of {26, 44}, of which the only sum of two squares is R = 26.

From the grid, 15ac = _425 = 65C + 800, so 65C = _625 and C must end in 5 (any number ending in 25 has a factor of 52, but 65 = 5×13 only has one 5 factor) and is one of {25, 45, 85} (not 65, which is Y); 65×45 = 2925 and 65×85 = 5525 don’t match _625 but 65×25 = 1625 does, so C = 25 and 15ac = 2425. This gives 2ac = 289 and 1dn = 324.

From 12ac, (D/20)2 = 16, so D = 80. From the grid, 13dn = 1040 + o2 = 65__, so o is between √(6500 − 1040) ≈ 73.9 and √(6599 − 1040) ≈ 74.6, ie o = 74 and 13dn = 6516. The first clue for 13dn gives (65, 1, E − 45), so E = √(65 − 1) + 45 = 45 ± 8 is one of {37, 53}. The square number at 19ac is now _6, and since 16 is used at 12ac, we must have 19ac = 36.

We know 14dn = 90 = 5 + O + t − 65, so O + t = 150, with both values ≥ 150 − 97 = 53. Then 5ac = (150 + Z − 74)2 for 2____ in the grid, so Z > √20000 − 76 ≈ 65.4, ie Z ≥ 68. For 10ac = (80 + O + Z − L)2 the maximum is (80 + 97 + 90 − 10)2 = 66049, to match _6169 in the grid. Testing the six possibilities, the only square number is 10ac = 56169 = 2372, so L = O + Z − 157, for which the maximum is 97 + 90 − 157 = 30, the only available values being {10, 17, 29}. As 19ac = 36 is the square of 2L + t − O = 2L + 2t − 150, t = (±6 + 150 − 2L)/2 and is one of {43, 49, 55, 61, 62, 68}, of which only {61, 68} are valid, with L being {17, 10} and O being {89, 82} respectively. Both options for Z = L − O + 157 give Z = 85, which makes 5ac = (150 + 85 − 74)2, ie 5ac = 25921.

Both options give L + t = 78, so the latter two expressions for 7ac are 78 − 65 = 13 and 10 + O + t = 160, and the sum of squares gives 7ac = 25769 = 5er − 41, so er = 5162 and both e and r are > 5162/97 ≈ 53.2, ie they are ≥ 58. The embedded 8ac = 576 = (55 + r − e)2, so r − e = ±24 − 55, ie e − r is one of {31, 79}; if the difference is 79, the minimum for e is 58 + 79 = 137, which is too high. Therefore e = r + 31, with a minimum of 58 + 31 = 89 and the only available values are {89, 90, 97}, of which only the first gives er = 5216, so e = 89 and r = 58.

The square at 4dn is _1, which can only be 4dn = 81, so 25 + W − 89 = ±9 and W is one of {55, 73}, of which only W = 73 is a sum of two squares. We can then enter 3dn = 9216 and 6ac = 6010.

For 18ac, the latter two expressions are L + t − A − C = 78 − 13 − 25 = 40 and DI − R − (L + t) = 80×5 − 26 − 78 = 296, so the sum of squares is 18ac = 89216 = 41t(85 − a), so a = 85 − 2176/t. If t is 61 then 2176/61 isn’t an integer, so t = 68, which makes a = 53 as well as L = 10 and O = 82. Now that 53 is taken, there’s only one option for E = 37.

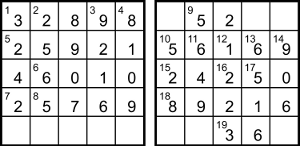Listener 4477 intermediate grid In the grid we have 2dn = 256, so 81 − N = ±16, ie N = 81 ± 16 is one of {65, 97}, but 65 is Y, so N = 97. Lastly, for 9ac we have 52 = (V − 48)2 + 62, so V = √(52 − 36) + 48 = 48 ± 4; 44 isn’t a sum of two squares, so V = 52. With all clues solved, the grids are partially filled, as shown here.

In numeric order, the letter values from clues are I = 5, L = 10, A = 13, P = 20, C = 25, R = 26, E = 37, M = 40, S = 41, T = 50, V = 52, a = 53, r = 58, Y = 65, t = 68, W = 73, o = 74, D = 80, O = 82, Z = 85, e = 89, N = 97, and we can separate the letters into the three parts ILAPCREMST, VarY, tWo DOZeN. Replacing the digits 0 to 9 with ILAPCREMST respectively, the grids are as shown below. As they are to contain 24 five-letter words, the four diagonals as well as the rows and columns must be included.

Listener 4477 partial grid As we must “vary” the positions of letters from the first grid to produce the second one, the letter counts must be the same in both grids. The first has AAAACEEIILLMPRRSSTTT and the second has AAAACEEEEILLPRRRSTT; to make them match, EER plus two more must be added to the first grid, and IMST plus two more to the second grid.

It’s easy to check in Chambers that the only words fitting the first and last down entries in the first grid are PACAS and SLITS, so the bottom row must be SEERS, also forming ARERE, STIME and TALER down, and PRIES and SAIRS in the diagonals. The second grid must now have IMSSST added; the only options for the second and fourth columns are RECTI and MERLE, leaving SSST for the corners. There are no words matching SRA??, to the T goes in the top-left cell and an S in each of the other corners, making TRAMS and SIPES across, TRASS and STIES down, and TEALS and SEATS diagonally.

Back to 2017 menu