Chessboard Carte Blanche by Hedgehog
Puzzle solution process
This is one possible solution path. The chessboard pattern means that all answers have alternating odd and even digits. From the answer lengths and grid symmetry, we can deduce immediately that the across entries are A to P and there are two in each row, with lengths of (4, 2), (4, 3), (5, 2), (3, 4), followed by the reverse lengths in the bottom half.
b and c are three-digit cubes, ie from the set {125, 216, 343, 729} (not 512 because it has consecutive odd digits). Y = 2c has four digits, so c = 729 and Y = 1458. E and L are opposite across entries with five digits, so they have the same pattern of odd-even digits (either both oeoeo or both eoeoe); we know L = E + b, so b = L − E and is even, which means b = 216.
There are only four four-digit Fibonacci numbers, {1597, 2584, 4181, 6765}, so H is one of {4181, 6765} (excluding consecutive digits of the same odd-even parity). As C = H + 729, C = 7494 (not 4910 with consecutive odd digits) and H = 6765.
F and T are factors of 6765; it has obvious factors of 5 and 3, and 6765/15 = 451 may be recognised as 11×41 (as the middle digit is the sum of the outer ones), so it’s fully factorised as 3×5×11×41. For F, the two-digit factors are {11, 15, 33, 41, 55}, of which only F = 41 has alternating parity. The three-digit factors are {123, 165, 205, 451, 615}, so T is one of {123, 165}. B is a factor of T − 3F, but 123 − 3×41 = 0, so T = 165. Now B is a two-digit factor of 165 − 3×41 = 42, ie one of {14, 21} (not 42 with consecutive even digits).
f = V + x (where x is a square), so the three-digit M = Vf = V2 + Vx, which means V < 32. V is also a two-digit factor of Y = 2×36, so it’s one of {18, 27}. If V is 27, adding squares {1, 4, 9, 16} gives {28, 31, 36, 43} respectively for f, of which only {36, 43} have alternating parity; but 27×36 = 972 for M has consecutive odd digits and 27×43 = 1161 is too big. So V = 18.
Now K = 18 + f and it’s the grid entry opposite F = 41, so its first digit is odd and the second is even, which means f is even. Then O = 2B + f is even, with a parity pattern of oe, and its opposite entry B has parity of eo, so B = 21, which makes R = 492.
Adding even squares {4, 16, 36, 64} to 18 for f, 18 + 4 = 22 has consecutive even digits, 18(18 + 36) = 972 for M has consecutive odd digits and 18(18 + 64) = 1476 is too big. So the square is 16, giving f = 34, M = 612, K = 52, O = 76 and a = 5610.
M has digit parity of eoe, so its opposite entry D is also eoe. But D shares the row with C = 7494, so there must be a space between them, with odd digits in grey cells and even digits in white ones. This allows us to place C, F, H, K and M in the grid and fix the positions of D, G, I, J and N .
From the grid, we know N’s parity pattern is eoeo, so P = N + 18 is also odd, with parity of eoeo, and must start in the fourth cell of the bottom row. Now we can place O = 76 in the first two cells of the bottom row, and its partner B = 21 at the end of the top row. A is opposite N, ie in cells 2 to 5 of the top row, and has parity of oeoe.
We know D = Q + 591 is even, so Q is odd. X = 165(Q − 18) has four digits, so Q ≥ 1010/165 + 18 ≈ 24.1, ie it’s at least 25. Q = e − 20, so e is odd and ≥ 45, and e = 18 + x needs x to be an odd square that’s ≥ 27. But 18 + 81 = 99 has consecutive odd digits, so x = 49, e = 67, Q = 47, D = 638 (which we can enter in the grid) and X = 4785. Now G = 769 (entered at the start of row 4), which makes S = 47678.
In row 2 of the grid we now have 7494_638, and for the first down answers Q to V we have {47, 492, 47678, 165, U, 18}, so it’s very likely that they all start in row 1, with 47 in column 1, 492 in column 3, 47678 in column 5, 165 in column 6, U in column 7 (where we already have 234) and 18 in column 8 (where we already have those digits). U = 234 is indeed 18×13 (ie V × a prime), and this placement of U and V matches the digits we have opposite being b = 216 and e = 67. But we’ll continue without this assumption.
The only three-digit values for d = 52x where x is a square are {52×4 = 208, 52×9 = 468, 52×16 = 832} and the only one with alternating digit parity is d = 832. That makes Z = 63232, J = 765 and I = 1638, and we can enter I and J in the grid.
W = (U − 165)2 has four digits, so U is between √1010 + 165 ≈ 196.8 and √9898 + 165 ≈ 264.5. It’s 18p where p is a prime, so p is between 10.9 and 14.7, ie one of {11, 13}, but 11×18 = 198 has consecutive odd digits, so p = 13, U = 234 and W = 4761.
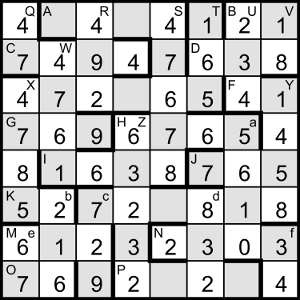
We now have all the down answers. With the digits we have in the grid, the only place Z = 63232 fits is at the bottom of column 4. The only other five-digit down answer is S = 47678, which must go opposite at the top of column 5. Then Q and R can only go at the tops of columns 1 and 3. Now the only place a = 5610 fits is down from the last grey cell in row 4, and Y = 1458 can only go in column 8, starting in row 3, which forces the 18 at the top of that column to be the entry for V, with T = 165 and U = 234 at the tops of column 6 and 7. The entries in the opposite corner are now forced to be b, c and e. All the down entries can be entered, giving the grid shown here.
In row 3, E could be 472_6 or 72_65, but we know it’s a multiple of T = 165, so it can’t end in 6. Of the five possibilities for 72_65 with an odd middle digit, the only multiple of 165 is E = 72765, which makes L = 72981 opposite.
Now N = 47x, where x is a square, is _303 in the grid, so x ends in 9 and is ≥ 2303/47 = 49 and ≤ 8303/47 ≈ 176.7, ie one of {49, 169}. But 47×169 = 7943 doesn’t fit, so N = 2303, which makes P = 2321. Finally, A = _4_4 and is a multiple of 41 and 67 (and 2, obviously). 4×41×67 = 10988 is too big, so A = 5494 = 2×41×67 and the grid is complete.
