Solitaire II by Xanthippe
Puzzle explanation
The words spelt out by playing the game, BECCAFICO, COB and DODO, are all types of bird, as is SOLITAIRE.
Puzzle solution process
This is one possible solution path. We’ll use the notation [XY] to mean any digit from the bracketed list or range.
The final 16 pegs spelling words can only have the digits A-F or 0-1, so the digits 2-9 must appear only once each in the grid (to be removed later as part of the countdown from F to 1).
The entries that are multiples of (hexadecimal) 10 must end in 0, and vice versa, so 0 can be entered at the end of 4ac, 11ac and 16ac/10dn, and no other entries end in 0.
The first move of the game of Solitaire takes the middle peg from one of 11ac, 12ac, 2dn or 15dn into the empty central cell. We’re told that the jumping and removed pegs have the same value, but of those four entries only 11ac has a repeated digit, so that’s where the first peg comes from. We already know it ends in 0, so 11ac is _00.
14ac and 15dn are both > E00, so they start with E or F. 13ac is odd, so it can’t end in E, so 14ac starts with F. It doesn’t have a repeated digit, so 15dn starts with E and 14ac is FE_; its digits are all letters and it’s even, so 14ac ends in one of [ACE]. 16ac has a repeated digit but it can’t be _00, because 9dn isn’t a multiple of 10, so 16ac is AA0 or CC0 (not EE0, because it has to be ≤ E00). AA0 (2720 in decimal) isn’t a multiple of 6, so 16ac = CC0 and 14ac = FEC.
13ac starts with an odd digit (because 5dn is odd), so to fit in the sequence 16ac (CC0) < 13ac < 15dn (E__) its first digit is D. Its middle digit is even (as 6dn is even) and 13ac is all letters, so it’s one of D[ACE]F. We can rule out DCF (in decimal, 3535 = 7 × 505) because 13ac isn’t a multiple of 7. 5dn has all odd-letter digits and 16ac < 5dn < 13ac, so 5dn = DBD (not DDD, as no entry has all three digits the same) and 11ac = B00. For 13ac to be > 5dn, DAF is now too small so 13ac = DEF.
As 16ac < 6dn < 5dn, 6dn starts with C or D, which makes 5ac D[CD]_. 5ac isn’t all letters, so its last digit is numeric (and even, but not 0); but 5ac has a repeated digit, which must be the D, so 5ac is one of DD[2468] and 6dn = D0E. We can rule out DD4 (3540 = 6 × 590) and DD6 (3542 = 7 × 506) because 5ac isn’t a multiple of 6 or 7.
We know 2dn < 3dn and both are between 11ac (B00) and 16ac (CC0), so 1ac is _[BC][BC]. As 1ac is even, it ends with C, not B. It also has a repeated digit, and both letter and number digits, so the number digit must be the first one and the repeated digit must be C in second and third place, ie, 1ac is [1-9]CC. As 2dn (C__) < 3dn (C0_), both are odd and 7ac contains only numeric digits, 2dn must be C0[1357] and 3dn is C0[3579]. 2dn is also a multiple of 7, so 2dn = C01.
As 9dn is between 3dn (C0[3579]) and 16ac (CC0) and it contains only letter digits, it’s C[AB]C. 16dn is between 3dn and 9dn and contains only letter digits, of which the second one is odd (because 17ac is odd), so 16dn is CB_, which forces 9dn = CBC. Then as 16dn is even, it can only be 16dn = CBA.
4ac contains all numeric digits and is a multiple of 6, so it’s [369]00. But 8ac is [3579]C_ and 8ac < 4ac, so 4ac can’t be 300 and 8ac can’t be 9C_. As 7ac < 8ac ([357]C_), 7ac can’t start with 8, so 7ac is 21[357], 7dn = 20F and 5ac = DD2. Note that this can be the only 2 in the grid. Now 1dn is [1-9][69]2, but 1dn < 7ac, so 1dn is 1[69]2 and 1ac = 1CC.
8ac is even and 10dn < 11ac (B00), so 10dn starts with [2468A]. 17ac has all odd digits and 4ac ([69]00) < 17ac < 10dn, so 17ac starts with [79] and 10dn starts with [8A]. 4ac can’t start with 9, because that would force 17ac to start with 9 a d there can’t be two 9s in the grid; so 4ac = 600 (making 1dn = 162). That prevents 8ac (< 4ac) from starting with 7, so for 8ac we have [35]C[8A], and the only combination that’s a multiple of 6 is 8ac = 5CA (making 7ac = 215 and 3dn = C05).
14dn is even and 18ac < 8dn (5_C), so 18ac starts with 4 (not 2, because the 2 already appears in 7ac).
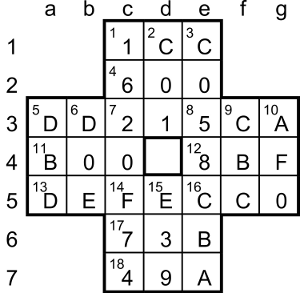
10dn is A_0, so it’s in the range A00 to AF0, which in decimal is 2560 to 2800. It’s a multiple of 64 (hexadecimal) = 100 (decimal), so it’s one of {2600, 2700, 2800}. But it’s also a multiple of 7, which only leaves 2800, so 10dn = AF0.
The four remaining indeterminate cells contain [3789] in some permutation. 12ac (_BF) doesn’t have all odd digits, so its first digit must the 8: 12ac = 8BF (making 8dn = 58C). Then 17ac (< 12ac) can’t start with 9, so it starts with 7 and 14dn = F74.
The options left for 15dn are E39 and E93; the latter (3731 = 7 × 533) is a multiple of 7, so 15dn = E39, making 17ac = 73B and 18ac = 49A. The grid is complete.
As we established at the start, the first move in the game of Solitaire is the jump from b4 to d4, removing the 0 at c4. For the next move, to remove an F, the only option is c6-c4.
We then have two moves that could remove an E: a5-c5 and e5-c5. The latter leaves no D available to be jumped, so we have to take a5-c5. Then the D can be jumped by either c4-c6 or d5-b5; the former leaves no C available, so we take d5-b5. The only move for the C is then f5-d5.
The three choices to jump a B are then a3-a5, f3-f5 and e7-e5; the first two don’t leave an A available, so we take e7-e5.
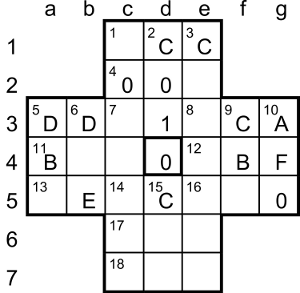
There are now two ways to jump an A: d5-f5 and e4-e6. If we choose d5-f5, the unique jumps available to remove the 9, 8, 7, 6 and 5 are c7-e7, e3-e5, c3-c5, c1-c3 and f5-d5, but that leaves the 4 in the e7 corner cell, unable to be jumped, so it’s a dead end. Therefore to remove the A we must choose e4-e6. The following unique available jumps are c7-e7 (9), e7-e5 (8), c3-c5 (7), c1-c3 (6) and e2-e4 (5).
There are now two ways to jump the 4 at e5: d5-f5 and e4-e6. The former leaves the 3 isolated in the d6 cell, unable to be jumped, so it’s a dead end. Therefore we must choose e4-e6 and the same peg makes the following unique available jumps: e6-c6 (3), c6-c4 (2). There are now two ways to jump a 1: c3-e3 and c4-c2. The preamble tells us that the same peg jumps the 2 and 1, so we must choose c4-c2. The grid is now as shown here.
As the first three letters of the 9-letter word can be jumped by the same peg, the possible sequences are g3-e3-c3-c1 (C10), e1-c1-c3-e3 (C01) and a3-a5-c5-e5 (BEC). We can rule out the first because the only word in Chambers starting with CIO is “cion”. After C01 the next jumpable peg would be B (a4 or f4), C (e3 or d5), D (b3) or 0 (d4), but there are no words in Chambers starting with COIB, COIC, COID or COIO, so the word must start with BEC.
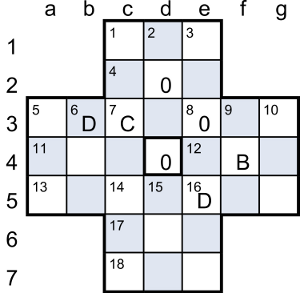
After a3-a5-c5-e5, the next jumpable peg is B (f4), C (d1 or f3) or 0 (d2 or d4). There are no words in Chambers starting with BECB, and all the ones starting with BECO have M as the next letter, which leaves only the birds BECCACCIA (a woodcock) and BECCAFICO (a garden warbler). The former isn’t possible because there’s only one A left, so the thematic word must be BECCAFICO.
For the second C in BECCAFICO there are two possible jumps: e1-c1 and g3-e3. If we choose e1-c1, it’s not possible to jump the A next, so we must choose g3-e3 (C), after which the only possible sequence is d3-f3 (A), g5-g3-e3 (FI), e1-c1 (C). There are then two choices of 0 to jump for the O in BECCAFICO: c1-c3 and c2-e2. The latter leaves a C stuck in the c1 corner, so we choose c1-c3, giving the position shown here.
Any jump involves two occupied adjacent cells in the grid. If we colour the grid like a chessboard, it’s clear that the D at b3 is the only digit on a different colour from the rest, so once it’s been jumped there will be no more jumps possible. Therefore the next sequence must be either b3-d3-f3-f5-d5-d3 (C0BD0) or b3-d3-d5-f5-f3-d3 (C0DB0), followed by d2-d4 (D) to leave the 0 from d2 in the centre. C0DB0D0 doesn’t make a pair of words, so the correct ending is C0BD0D0, giving COB (a gull (archaic) or male swan) and DODO, both birds, like BECCAFICO and SOLITAIRE (gigantic flightless pigeon).
