Pentomino Factory by Oyler
Detailed Solution
The first step is to find what the base pentominoes look like, ie, the 12 shapes that are distinct whatever rotations and reflections are used. These have been given names, sometimes rather fanciful, in various ways. The picture below uses the original names (due to Solomon Golomb), but only for reference purposes in the text that follows.
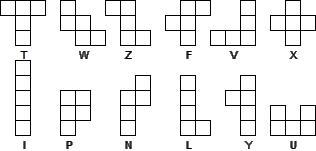
We also need a table of factors for each “clue”.
| Row | Column | ||||
|---|---|---|---|---|---|
| No | Clue | Factors | No | Clue | Factors |
| 1 | 1,497,375,000 | 23 . 32 . 56 . 113 | 1 | 4,356 | 22 . 32 . 112 |
| 2 | 14,701,500 | 22 . 35 . 53 . 112 | 2 | 12,474 | 2 . 34 . 7 . 11 |
| 3 | 15,246 | 2 . 32 . 7 . 112 | |||
| 4 | 3,150 | 2 . 32 . 52 . 7 | |||
| 8 | 1,536 | 29 . 3 | |||
| 9 | 32 | 25 | |||
| 10 | 640 | 27 . 5 | |||
| 11 | 8,640 | 26 . 33 . 5 | |||
| 12 | 36,000 | 25 . 32 . 53 | |||
We start with the 11s and these must appear in the top left-hand portion of the grid. Hence the letter B is entered at r1c1, r1c2, r1c3, r2c1 and r2c3, to give the U pentomino.
As only three 7s appear, two must be in the annihilated region and are in either the I or L pentomino. The remaining four cells in c2 can be either (2, 7, 9, 9) or (3, 6, 7, 9) in some order. It cannot be the latter as r2c2 would then be isolated. Thus c3 must have 2 or 9 and must contain (2, 7, 9) in some order. This allows us to fit in 9s in c2 and c3.
Since there is no room for 3s, c1 must be (2, 2, 9). This fixes 9 in r3c4 and 9 must be the Y pentomino. This tells us that 2 is the L pentomino and 7 is the I pentomino, though not where they lie.
c4 must be (2, 7, 9, 5, 5) and row factorisations show the 5s are in r1c4 and r2c4.
Now consider c10, c11 and c12. These must contain 10s, with three in c12. Hence c12 is (10, 10, 10, 6, 6) since 9s are already placed elsewhere. Consider r1: it must be completed with 3 x 5, 3 x 10 and (3, 3, 1) since the L pentomino is unavailable. Hence 10 (written as A) is the V pentomino and 5 is the P pentomino since the only other viable shape is taken by 11.
There are no 6s in c10, so the others must be in c11, giving the N pentomino, with 4 as the final element. c10 must have a 4, leaving 16. It can’t have a 2 so this must be 4 x 4. Therefore 4 is the T pentomino with 1 left for the final entry.
The rest of c9 is 8, which must be (8, 1, 1). We can’t have 8 in r1, so the column is (1, 1, 1, 8, 4).
r2 has (3, 3, 1) left. The one is fixed, giving 1 as the X pentomino.
This leaves W, Z and F for 0, 8 and 3. Examine c8: (3, 1, 8, 8, 8). This fixes 0 as the Z pentomino. 8 can’t be W, so must be the F pentomino. Hence, 3 is the W pentomino.
r3c5 must be 0, being too far from 2 or 8, so r4c5 is also 0, to be connected. This fixes 2 and 7.
r4c6 is 0 and so is r4c7 and r4c8, implying r3c7 is 8.
Let B be G(reen) and 9 be R(ed). Then 5 must be different, B(lue) say. Trying to avoid a fourth colour, 0 must be G. Then 2 must be B and 7 must be R. 3, different from 0 and 5, must be R, so 8 is B and 1 is G. Finally, 4 must be R, 6 must be B and A must be R.
